源码阅读之LinkedList实现细节

0x00 描述

LinkedList 是一个双向链表，这是一个基础的数据结构。打开 LinkedList 源码，可以看到它继承于 AbstractSequentialList ，这个是 AbstractList 的子类。同时也实现了 List 、Deque 、Clone、Serializable 接口。所以简化的类关系图可以表示为

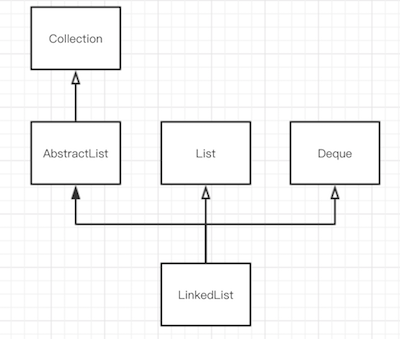
linkedlist-structure

关键属性

size 记录当前数组元素的个数
first 链表头指针
last 链表尾部指针
modCount 记录修改次数，这个字段是继承于 AbstractList

LinkedList 是实现了序列化接口 Serializable ，而以上属性都被声明为 transient 表示这些字段不参与序列化。

节点

private static class Node<E> {
	E item;
	Node<E> next;
	Node<E> prev;

	Node(Node<E> prev, E element, Node<E> next) {
		this.item = element;
		this.next = next;
		this.prev = prev;
}

这个节点类，记录链表中的节点的数据，有前指针、后指针和具体的数据元素。这个数据这里用泛型来表示了。

构造方法

public LinkedList() {
}

这个是默认构造函数，创建一个空链表。

public LinkedList(Collection<? extends E> c) {
	this();
	addAll(c);
}

这是通过列表来创建链表的。它调用了 addAll 方法。这个方法后文会讲到。

0x01 常用方法

addFirst(E e)

在链表头部添加节点

public void addFirst(E e) {
	linkFirst(e);
}

private void linkFirst(E e) {
	final Node<E> f = first;
	final Node<E> newNode = new Node<>(null, e, f);
	first = newNode;
	if (f == null)
		last = newNode;
	else
		f.prev = newNode;
	size++;
	modCount++;
}

它实际是调用了内部的一个私有方法 linkFirst 。只需要改变指针指向，时间复杂度O(1)。

addLast(E e)

public void addLast(E e) {
	linkLast(e);
}

void linkLast(E e) {
	final Node<E> l = last;
	final Node<E> newNode = new Node<>(l, e, null);
	last = newNode;
	if (l == null)
		first = newNode;
	else
		l.next = newNode;
	size++;
	modCount++;
}

在链表尾部添加一个节点。它也是内部的 linkLast 方法。这方法执行效率也很高，只需要改变指针指向，时间复杂度是O(1)。

add(E e)

public boolean add(E e) {
	linkLast(e);
	return true;
}

可以看出也是调用了 linkLast 方法。

add(int index, E element)

public void add(int index, E element) {
	checkPositionIndex(index);

	if (index == size)
		linkLast(element);
	else
		linkBefore(element, node(index));
}

private void checkPositionIndex(int index) {
	if (!isPositionIndex(index))
		throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}

private boolean isPositionIndex(int index) {
	return index >= 0 && index <= size;
}

在某个 index 前插入元素。

首先它会检查 index 是否正确。如果在 0~size 范围内的下标，那么就执行插入的方法；

它会判断如果 index 是等于 size 那么就在尾部插入元素，否则就在 index 所在节点前面插入元素。

void linkBefore(E e, Node<E> succ) {
	// assert succ != null;
	final Node<E> pred = succ.prev;
	final Node<E> newNode = new Node<>(pred, e, succ);
	succ.prev = newNode;
	if (pred == null)
		first = newNode;
	else
		pred.next = newNode;
	size++;
	modCount++;
}

这个方法在节点 succ 前面添加元素，时间复杂度为O(1)。

在调用这个方法之前需要获取到节点

Node<E> node(int index) {
	// assert isElementIndex(index);

	if (index < (size >> 1)) {//size >> 1 相当于 size/2
		Node<E> x = first;
		for (int i = 0; i < index; i++)
			x = x.next;
		return x;
	} else {
		Node<E> x = last;
		for (int i = size - 1; i > index; i--)
			x = x.prev;
		return x;
	}
}

在链表中要通过下标查找一个节点，需要通过遍历。这里做了一个优化，当 index 是在前半部分时从链表头部开始遍历；如果 index 超过当前链表的一半时则从后面开始遍历查询，它的时间复杂度为O(n)。

addAll(Collection<? extends E> c)

public boolean addAll(Collection<? extends E> c) {
	return addAll(size, c);
}

在尾部插入一个列表，通过调用 add(int,Collection) 来实现。

addAll(int index, Collection<? extends E> c)

public boolean addAll(int index, Collection<? extends E> c) {
    //先检测 index 是否有效
    checkPositionIndex(index);
	
    //以数组的形式获取到列表数据
	Object[] a = c.toArray();
	int numNew = a.length;
	if (numNew == 0)
		return false;
	//找到index的前向指针，后向指针
	Node<E> pred, succ;
	if (index == size) {
		succ = null;
		pred = last;
	} else {
		succ = node(index);
		pred = succ.prev;
	}
	//依次把数组中的节点插入到列表中
	for (Object o : a) {
		@SuppressWarnings("unchecked") E e = (E) o;
		Node<E> newNode = new Node<>(pred, e, null);
		if (pred == null)
			first = newNode;
		else
			pred.next = newNode;
		pred = newNode;
	}
	//链接后向指针
	if (succ == null) {
		last = pred;
	} else {
		pred.next = succ;
		succ.prev = pred;
	}
	//更新size和modCount
	size += numNew;
	modCount++;
	return true;
}

这个方法稍微复杂一点

先检测 index 是否有效
以数组的形式获取到列表数据
找到 index 所在节点的前向指针，后向指针
依次把数组中的节点插入到列表中
链接后向指针的数据
更新 size 和 modCount

get(int index)

public E get(int index) {
	checkElementIndex(index);
	return node(index).item;
}

获取 index 所在元素，通过 node 方法获取。前面分析可以知道，这个方法需要遍历，它的时间复杂度是O(n)。

contains(Object o)

public boolean contains(Object o) {
	return indexOf(o) != -1;
}

public int indexOf(Object o) {
	int index = 0;
	if (o == null) {
		for (Node<E> x = first; x != null; x = x.next) {
			if (x.item == null)
				return index;
			index++;
		}
	} else {
		for (Node<E> x = first; x != null; x = x.next) {
			if (o.equals(x.item))
				return index;
			index++;
		}
	}
	return -1;
}

查询某个对象是否存在于该链表中是通过遍历来实现的。

peek()

查看链表头节点

public E peek() {
	final Node<E> f = first;
	return (f == null) ? null : f.item;
}

peekFirst()

查看链表头节点

public E peekFirst() {
	final Node<E> f = first;
	return (f == null) ? null : f.item;
}

peekLast()

查看链表尾部节点

public E peekLast() {
	final Node<E> l = last;
	return (l == null) ? null : l.item;
}

poll()

获取头节点，并把头节点从链表中删除

public E poll() {
	final Node<E> f = first;
	return (f == null) ? null : unlinkFirst(f);
}

private E unlinkFirst(Node<E> f) {
	// assert f == first && f != null;
	final E element = f.item;
	final Node<E> next = f.next;
	f.item = null;
	f.next = null; // help GC
	first = next;
	if (next == null)
		last = null;
	else
		next.prev = null;
	size--;
	modCount++;
	return element;
}

pollFirst()

同上

public E pollFirst() {
	final Node<E> f = first;
	return (f == null) ? null : unlinkFirst(f);
}

pollLast()

获取尾部节点，并将尾部节点删除

public E pollLast() {
	final Node<E> l = last;
	return (l == null) ? null : unlinkLast(l);
}

private E unlinkLast(Node<E> l) {
	// assert l == last && l != null;
	final E element = l.item;
	final Node<E> prev = l.prev;
	l.item = null;
	l.prev = null; // help GC
	last = prev;
	if (prev == null)
		first = null;
	else
		prev.next = null;
	size--;
	modCount++;
	return element;
}

remove()

删除头节点

public E remove() {
	return removeFirst();
}
public E removeFirst() {
	final Node<E> f = first;
	if (f == null)
		throw new NoSuchElementException();
	return unlinkFirst(f);
}

clear()

清空链表

public void clear() {
	// Clearing all of the links between nodes is "unnecessary", but:
	// - helps a generational GC if the discarded nodes inhabit
	//   more than one generation
	// - is sure to free memory even if there is a reachable Iterator
	for (Node<E> x = first; x != null; ) {
		Node<E> next = x.next;
		x.item = null;
		x.next = null;
		x.prev = null;
		x = next;
	}
	first = last = null;
	size = 0;
	modCount++;
}

遍历整个链表，将节点中的数据置为 null 。

0x02 总结

LinkedList 是一个双向链表，它是线程不安全的。
LinkedList 擅长插入、删除操作，时间复杂度是O(1)；但是如果事先不知道被插入的节点，则需要通过遍历来查询到该节点，而查询操作就不是很高效了，时间复杂度是O(n)。
get 方法需要遍历获得，containts 方法也需要遍历
在链表头部或尾部插入节点效率要高，但是通过下标 index 插入节点则需要遍历找到插入的位置，再执行插入操作。

Published on Oct 17, 2018 in categories 数据结构

上一篇源码阅读之ArrayList实现细节
下一篇源码阅读之Java栈的实现